Фрактальное планирование, или окончательное не-решение вопроса о сроках и стоимости дизайн-проектов

Допустим, к вам приходит Некто и говорит — хочу проект. Вот такой:

А вы ему — да не вопрос, но, может быть, по случаю субботы доуточним кое-какие требования? Примерно так:

Некто соглашается и даже развивает вашу мысль:

Вы тоже не хотите ударить в грязь лицом:

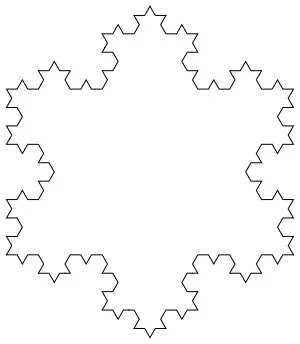
Общий тренд обоим понятен, собеседники счастливо смеются.

И тут Некто делает ход конём — спрашивает, когда и почём.

Вы прикидываете: ну, в квадратный метр конструкция вписывается. Некто угукает, и вы стартуете…

Что вы стартуете? Огораживание территории проекта. Выпиливание его контуров аккуратным лобзиком. Или просто вырезание из бумаги, тоже красиво. В общем, поход вдоль снежинки Коха (вы ведь именно о ней договорились, сами того не зная).

У меня для вас плохие новости: хотя снежинка Коха и вписывается в пресловутый квадратный метр, но её длина — бесконечна.

Не дойдёте никуда, короче, если будете слишком уж придерживаться договорённостей.

Значит, обман? Или что?

Меня как бывшего математика уже полтора часа (а как настоящего менеджера — уже много-много лет) занимает вопрос: и как же в таких нечеловеческих, но вполне моделируемых чудо-наукой условиях планировать производство и обсчитывать бюджет?

А главное, как всё-таки вдоль этой дурацкой кривой двигаться без кровавых жертв?

Нагуглилось ровно три занятных ссылки:

1. [Fractals and What They May Offer Project Management](https://www.academia.edu/7155783 For_Fractals_and_What_They_May_Offer_Project_Management)
2. The Fractal Method of Project Management
3. Использование фрактальной теории в стратегическом планировании и управлении

Впрочем, всё это неважно.

Ведь в наших головах так хорошо зашит парадокс Зенона об Ахиллесе и черепахе и его счастливое разрешение, что мы всегда думаем: да ладно, ведь всего-то и нужно, что ещё немного времени…

Ерунда. Не работает классическая метафора. И мы это знаем отлично. Но продолжаем наступать на фрактальные грабли.

Извините, я не про обрезание функционала и прочие очевидные действия, позволяющие дожать проект. Я про то, как применить понимание его фрактальной природы при планировании на старте.

Ведь уже давно понятно, что подход «Мы стали более лучше собирать требования в начале проекта», мягко говоря, несколько наивен.

Ну оценим мы длину границы очередной линии, экстраполирующей фрактал. Типа, «Пяти спринтов тут достаточно» (извините, что agile, сама не хочу, но так проще проиллюстрировать итеративные приближения).

А как при этом измерить расстояние от этой линии до неизвестной нам целевой, описывающей финальную стадию проекта? В каких практически применимых попугаях? Явно эти расстояния имеют отношение к понятию «качество», но — какое?

Сможем ли мы, использовав знание об этом расстоянии, оценить длину конечной версии контура? И, главное, как не выскочить из коридора?

Подсказывают из зала ключевое слово «Фрикономика». Не читала пока, не знаю. Да и вряд ли там много математики — а тут её как раз вагон должно быть.

И, видимо, излишне говорить, что такое поведение проекта — наверняка есть суть (человеческой) природы, бороться с ним бесполезно и глупо.

Какая суть, что за суть? Я не знаю, это отдельный вопрос.

Но точно знаю, что делать на старте оценку проекта, даже очень маленького, всё более «точными» старыми дискретными методами — это примерно как пытаться улететь к Солнцу на первой космической скорости. Поизмеряйте, если такова ваша религия, я же — пас.

Самое же страшное, от чего реально сносит крышу, — это то, что целевая линия любой длины всё же ограничивает отнюдь не бесконечный кусок плоскости. То есть при потенциально бесконечном объёме работ мы всё равно получим заведомо конечный результат.

В общем, умному ассоциаций достаточно. Рассказывайте, кто что знает?

Бонус — сравните снежинки Коха после 5-й и 6-й итераций:

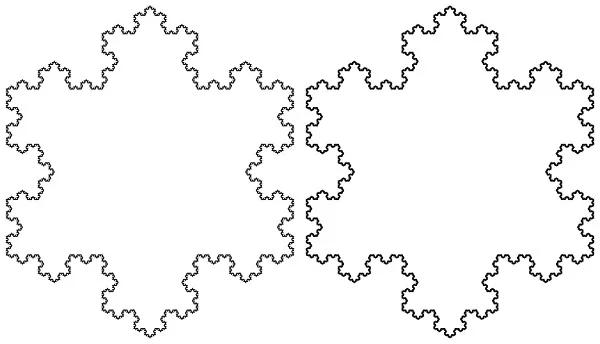
По-моему, хорошо видно, что после 5-й итерации начинается вышивание бисером по шоколаду. А оно мало кому по средствам.

Да, все картинки любезно предоставлены генератором снежинок Коха системы WolframAlfa.

P. S. А кто напишет, что снежинка Коха есть контур бесконечной длины, очерчивающий фигуру конечной площади, того в Википедии забанят пожизненно :)